Difference between revisions of "The Sensitivity Analysis Library"
| Line 18: | Line 18: | ||
Abstracts of these talks are at [[Analytica User Group/Past Topics]]. | Abstracts of these talks are at [[Analytica User Group/Past Topics]]. | ||
| − | = | + | = What is Computed = |
| + | |||
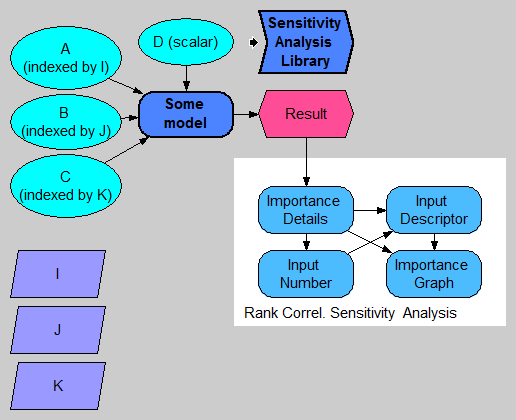
| + | The following diagram depicts a model having four uncertain inputs, ''A, B, C, '' and ''D'', of which ''A, B,'' and ''C'' are array-valued with various indexes (pay attention to the top-left). The model computes ''Result''. | ||
[[image:Sensitivity functions ex1.png]] | [[image:Sensitivity functions ex1.png]] | ||
| − | The library looks for chance nodes that are ancestors of the result being analyzed. You will want to make sure that the inputs you want to vary are defined as chance nodes, and are probabilistic. | + | Because we are considering every cell of every input array, there could in general be a huge number of inputs to depict. It is therefore of value to direct our attention only to the few inputs having the greatest sensitivity. |
| + | |||
| + | The Sensitivity Analysis Library is applicable when we are interested in knowing which scalar input values (i.e., which array cells) the result is most sensitive to. The following chart shows an example where the five most sensitive input cells are depicted. The bar size gives an indication of the relative sensitivity of the output to each of these input cells: | ||
| + | |||
| + | [[image:Importance graph 5top.png]] | ||
| + | |||
| + | Notice that in the chart ''C[K=iv]'' has a negative value. This indicates that an increase in that value would cause a decrease in the result. Because that bar is roughly twice as large as the one for ''A[I=6]'', the graph indicates that the output is roughly twice as sensitive to changes in ''C[K=iv]'' as it is to changes in ''A[I=6]''. | ||
| + | |||
| + | The exact value depicted by the each bar can reflect different types of sensitivity information. These different types of information may be interpreted in various ways, depending on which metric is used. The library comes with three measures that can be readily used: [[RankCorrel|Rank Correlation]], [[Regression|General Regression Coefficients]], and Stepwise Regression coefficients. [[RankCorrel|Rank Correlation]] is a good indicator of how much the uncertainty in the input contributes to the uncertainty in the output. Regression coefficients are indicators of how much a 1% change in the input will change the output. All three of these metrics are instances of ''global sensitivity analyses''. | ||
| + | |||
| + | = How to Use = | ||
| + | |||
| + | The library looks for chance nodes that are ancestors of the result being analyzed. You will want to make sure that the inputs you want to vary are defined as chance nodes, and are probabilistic. | ||
To implement a sensitivity analysis based on this library, you will typically add four nodes to your model. In the above diagram, these are ''Importance_details'', ''Input_number'', ''Input_descriptor'', and ''Importance graph''. Each of these four is defined using a function from the library. | To implement a sensitivity analysis based on this library, you will typically add four nodes to your model. In the above diagram, these are ''Importance_details'', ''Input_number'', ''Input_descriptor'', and ''Importance graph''. Each of these four is defined using a function from the library. | ||
Revision as of 02:58, 18 April 2008
The Sensitivity Analysis Library provides functions that help you create sensitivity analyses of models containing array-valued inputs.
The functions in this library allow you to compute the sensitivity of a result to each cell of each array-valued uncertain input. It is similar to Make Importance (on the Object menu), except that Make Importance varies each chance array input as a whole, while the functions in this library vary each individual cell of array-valued input variables.
Download
To use, download the library from Sensitivity Analysis Library.
The Sensitivity Functions Examples.ana model demonstrates the use of this library.
Webinar on Using It
You can watch recordings of two webinars that cover the topic of setting up and graphing sensitivity analyses:
The first webinar is a pre-requisite for the second. The last part of the second webinar introduces this library and demonstrates its usage.
Abstracts of these talks are at Analytica User Group/Past Topics.
What is Computed
The following diagram depicts a model having four uncertain inputs, A, B, C, and D, of which A, B, and C are array-valued with various indexes (pay attention to the top-left). The model computes Result.
Because we are considering every cell of every input array, there could in general be a huge number of inputs to depict. It is therefore of value to direct our attention only to the few inputs having the greatest sensitivity.
The Sensitivity Analysis Library is applicable when we are interested in knowing which scalar input values (i.e., which array cells) the result is most sensitive to. The following chart shows an example where the five most sensitive input cells are depicted. The bar size gives an indication of the relative sensitivity of the output to each of these input cells:
Notice that in the chart C[K=iv] has a negative value. This indicates that an increase in that value would cause a decrease in the result. Because that bar is roughly twice as large as the one for A[I=6], the graph indicates that the output is roughly twice as sensitive to changes in C[K=iv] as it is to changes in A[I=6].
The exact value depicted by the each bar can reflect different types of sensitivity information. These different types of information may be interpreted in various ways, depending on which metric is used. The library comes with three measures that can be readily used: Rank Correlation, General Regression Coefficients, and Stepwise Regression coefficients. Rank Correlation is a good indicator of how much the uncertainty in the input contributes to the uncertainty in the output. Regression coefficients are indicators of how much a 1% change in the input will change the output. All three of these metrics are instances of global sensitivity analyses.
How to Use
The library looks for chance nodes that are ancestors of the result being analyzed. You will want to make sure that the inputs you want to vary are defined as chance nodes, and are probabilistic.
To implement a sensitivity analysis based on this library, you will typically add four nodes to your model. In the above diagram, these are Importance_details, Input_number, Input_descriptor, and Importance graph. Each of these four is defined using a function from the library.
- Importance_details does almost all the work. It locates all the chance input variables, flattens them to the cell level, assembles their input values, and computes the sensitivity of the result to each of input cells.
- Input_number: Because the number of input cells is likely to be huge, we usually want to restrict attention to a small subset of input cells -- those input cells that the output is most sensitive to. Inside Input_number, we specify how many inputs we want to include. The result is just a sequence 1..N.
- Input_descriptor: Assembles meaningful names for each input cell. To meaningfully identify each input cell, we need to indicate the variable name along with the coordinate of the cell. These input names use a Subscript-like description.
- Importance_graph: This is the final result graph.
(This page is not completely filled in)
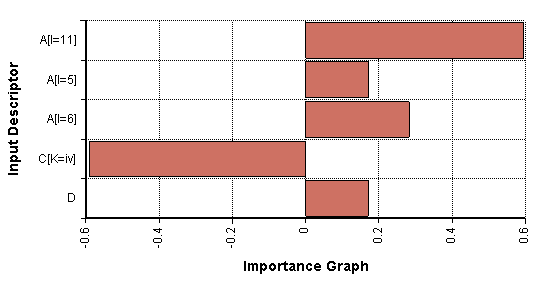
Enable comment auto-refresher