Difference between revisions of "IPmt"
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:Financial Functions]] | [[Category:Financial Functions]] | ||
| − | [[Category:Doc Status | + | [[Category:Doc Status C]] <!-- For Lumina use, do not change --> |
| − | |||
| − | |||
| + | == IPmt(rate, per, nper, pv'', fv, type'') == | ||
Returns the interest portion of a payment received on an annuity, assuming constant periodic payments and a fixed interest rate. | Returns the interest portion of a payment received on an annuity, assuming constant periodic payments and a fixed interest rate. | ||
Parameters: | Parameters: | ||
| − | + | ;«Rate»: The interest rate per period. | |
| − | + | ;«Per»: The period to compute the principal payment for. {1..«NPer»} | |
| − | + | ;«NPer»: The total number of periods in the annity's lifetime. | |
| − | + | ;«Pv»: The present value. | |
| − | + | :If you receive a loan, this is the loan amount as a positive number. | |
| − | + | :If you give someone a loan, this is a negative number. | |
| − | + | ;«Fv»: (Optional) Future value of annuity at the end of «NPer» periods. | |
| − | + | :If you receive a loan, this is your final balloon payment at the end as a negative number. | |
| − | + | :If you get money back at the end, this is a positive number. | |
| − | + | ;«Type»: (Optional) Indicates whether payments are at the beginning of the period. | |
| − | + | :<code>True</code> = Payments due at beginning of period, with first payment due immediately. | |
| − | + | :<code>False</code> = Payments due at end of period. (default) | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | == Library == | ||
Financial Functions | Financial Functions | ||
| − | = Examples = | + | == Examples == |
| − | |||
You have a 30-year fixed-rate mortgage at 6.5% on an initial loan amount of $350K. You have held the mortgage for 5 years -- your next payment will be the 61th payment. How much of your current monthly payment goes towards interest? | You have a 30-year fixed-rate mortgage at 6.5% on an initial loan amount of $350K. You have held the mortgage for 5 years -- your next payment will be the 61th payment. How much of your current monthly payment goes towards interest? | ||
| − | :-IPmt(6.5%/12,61, 30*12,$350K) → $1774.71 | + | :<code>-IPmt(6.5%/12, 61, 30*12, $350K) → $1774.71</code> |
As a percent of the monthly payment: | As a percent of the monthly payment: | ||
| − | :IPmt(6.5%/12,61,30*12,$350K) / | + | :<code>IPmt(6.5%/12, 61, 30*12, $350K)/Pmt(6.5%/12, 30*12, $350K) → 80%</code> |
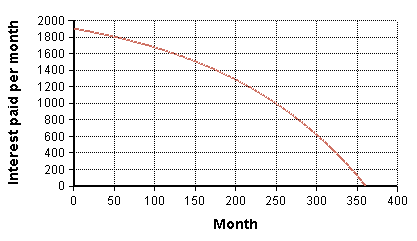
Create a graph of interest paid each month during the life time of the loan. | Create a graph of interest paid each month during the life time of the loan. | ||
| + | :<code>Index Month := 1..30*12</code> | ||
| + | :<code>-IPmt(6.5%/12, Month, 30*12, $350K) →</code> | ||
| − | : | + | :[[Image:Ipmt per month.png]] |
| − | |||
| − | |||
| − | |||
| − | * [[PPmt]] | + | == See Also == |
| + | * [[PPmt]] | ||
| + | * [[Pmt]] | ||
* [[CumIPmt]] | * [[CumIPmt]] | ||
| − | * [[Rate]] | + | * [[Rate]] |
| + | * [[NPer]] | ||
| + | * [[Pv]] | ||
| + | * [[Financial functions]] | ||
Latest revision as of 00:55, 30 January 2016
IPmt(rate, per, nper, pv, fv, type)
Returns the interest portion of a payment received on an annuity, assuming constant periodic payments and a fixed interest rate.
Parameters:
- «Rate»
- The interest rate per period.
- «Per»
- The period to compute the principal payment for. {1..«NPer»}
- «NPer»
- The total number of periods in the annity's lifetime.
- «Pv»
- The present value.
- If you receive a loan, this is the loan amount as a positive number.
- If you give someone a loan, this is a negative number.
- «Fv»
- (Optional) Future value of annuity at the end of «NPer» periods.
- If you receive a loan, this is your final balloon payment at the end as a negative number.
- If you get money back at the end, this is a positive number.
- «Type»
- (Optional) Indicates whether payments are at the beginning of the period.
True= Payments due at beginning of period, with first payment due immediately.False= Payments due at end of period. (default)
Library
Financial Functions
Examples
You have a 30-year fixed-rate mortgage at 6.5% on an initial loan amount of $350K. You have held the mortgage for 5 years -- your next payment will be the 61th payment. How much of your current monthly payment goes towards interest?
-IPmt(6.5%/12, 61, 30*12, $350K) → $1774.71
As a percent of the monthly payment:
IPmt(6.5%/12, 61, 30*12, $350K)/Pmt(6.5%/12, 30*12, $350K) → 80%
Create a graph of interest paid each month during the life time of the loan.
Index Month := 1..30*12-IPmt(6.5%/12, Month, 30*12, $350K) →
See Also
Comments
Enable comment auto-refresher