Array Manipulation Examples and Challenge Problems
This page is a place to collect array-manipulation examples and challenge problems.
If you are learning to use Analytica, try these challenge problems before looking at the solutions.
If you have an example that might be helpful to others, post it!
These should be problems that can be described concisely, and are focused on manipulations of arrays. Beyond the scope would be questions like how to model some particular problem, or how to structure a problem.
List and 1-D manipulations
Reversing a list
Given: Index I, as a list of labels.
Define: Index I_rev containing the same labels as I, but in reverse order.
Solution 1
Define I_rev as
Slice(I, size(I)..1)
Solution 2
Test yourself: Why is the CopyIndex required here?
Reversing an array
Given: Array A, indexed by I.
Compute: A_rev, also indexed by I, but with the order of elements along I reversed.
Solution 1
Define A_rev as
A[@I = size(I) - @I + 1]
Solution 2
Reverse(A, I)
Reversing two halves of an array separately
Given:
- Array
A, indexed byI. - N: A position along I
Compute: Reverse the first N elements of A, and separately reverse the remaining elements of A after the Nth.
The model Reverse_halves.ana sets up the problem, shows the desired final result, and provides a variable for you to define with your solution. In the Solutions module, it also shows two possible solutions (don't peek until you've attempted it yourself!).
Move nulls to end
Given an array with scattered Null cells, move all the nulls to the end along index I, compressing the non-null elements to the start along I but in the same order.
The model file Move nulls to end.ana contains the setup, the desired result, and one possible solution.
Re-indexing
Re-indexing refers to operations that produce a new array with the same data, but on different indexes than the original.
The exercises here are pretty simple, but illustrate extremely common re-indexing operations that you are likely to use over and over again in your own models. Load the model here and fill in the Definitions of the undefined nodes. When you are done, compare your solutions to the ones given in the Solutions sub-module.
Model file: Re-indexing challenges.ana
Arithmetic
Implement a counter
You are to write an expression that counts in a given base. Each digit is separated into a separate "column" along a digit index.
The model file Counting challenge.ana sets up the indexes that you'll need, so that you just need to fill in one Definition. There is a really simple solution to this one -- fewer than 30 characters in length -- if you are thinking in terms of arrays and array abstraction.
Table Lookups
Includes 2-step lookup, aka outer-product.
Look-up in a 2-D table
In this challenge, you must convert a Gregorian calendar date (the western calendar) into a date on the Islamic Hijri calendar. This is a challenge in performing a look-up in a 2-D table.
The Hijri calendar is a lunar calendar with 12 months per year, each month containing 29 or 30 days and starting just after the new moon. The process for determining when a new month starts is rather contorted and not even consistent between Muslim countries, but do not fear -- we provide you with a table that gives you the Gregorian date for the first day of each Hijri month.
Suppose the Gregorian date is 8-July-2014. You need to look in the supplied table (First_day_of_month) to find which Islamic year and month this would fall in. For example, the table shows
First_day_of_month[Islamic_year = 1435, Islamic_month = 9] → 28-June-2014First_day_of_month[Islamic_year = 1435, Islamic_month = 10] → 28-July-2014
We can thus see that 8-July-2014CE falls in the 9th month (Ramadan) of the year 1434AH, and since that month starts on 28-June-2014, 8-July is the 11th day. Hence, the Hajri date would be 1435/9/11 or 1435-Ramadan-11.
The model file Islamic date conversion.ana contains the challenge. Load this model, then fill in the hashed nodes with the expressions required to complete the look-up. If you need to create additional variables as well, this is allowed.
One possible solution is provided in Islamic date conversion solution.ana. Other approaches are also possible.
Array Reduction
Reduction between a start and stop point
Sum only the daily amounts landing between start and stop dates. Daily amounts, start and stop all vary by Person. Open the model and fill in the Definition of the one undefined variable. A correct solution is provided.
Model file: Sum between.ana (contains setup and solution)
Flattening and Un-flattening
Transform a Date index to 3-D
Given data indexed by a flat date index, with dates 1-Jan-2015 .. 31-Dec-2020, transform this data into a 3-D array indexed by Year, Month and Hour. This in an example of "unflattening" a 1-D array into a 3-D array.
Model file: Date index to 3D.ana (contains setup, example data, and solution).
Load the model file here. The indexes are set up for you and the starting data is given. You need to create and define a variable that performs the desired unflattening. You may want to use more than one variable in your solution.
Flattening a 2-D matrix to a 1-D vector
Given: Array A[I, J], indexed by I and J.
Compute: 1-D Array B[K], where K has length Size(I)*Size(J), containing the elements of A.
Model file: Flattening 2-D to 1-D.ana (contains setup and solutions)
The need to flatten a matrix into 1-D occurs in several contexts. When setting up an optimization, for example, the decision variables must be collected into a single 1-D vector. If you are finding the optimal weight-matrix, for example, you may need to "flatten" your initial guess, in order to pass it to NlpDefine. Similarly, you may have a 2-D array of coefficients identified in a Regression problem, that must be flattened into a 1-D basis index.
Solution 1
Demonstrated in the Solution_1 module of Flattening 2-D to 1-D.ana.
- Add Library..., Concatentation.ana
- Define
Kas:K := 1..Size(I)*Size(J) - Define
BasConcatRows(A, I, J, K)
Solution 2
This is the more general solution, in that it generalized to flattening N-D arrays.
Demonstrated in the Solution_2 module of Flattening 2-D to 1-D.ana.
- Define
Kas:K := 1..Size(I)*Size(J) - Define
L := ['I', 'J', 'A'] - Define
B := MdArrayToTable(A, K, L)[L = 'A']
Solution 3
Demonstrated in the Solution_3 module of Flattening 2-D to 1-D.ana.
- Define
Kas:K := 1..Size(I)*Dize(J) - Define
Bas:A[@I = floor((@K - 1)/size(J) + 1), @J = Mod((@K - 1), size(J)) + 1]
Unflattening a 1-D vector into a 2-D array
Given: Vector B, indexed by K. Also indexes I, J. The index K has Size(I)*Size(J) elements.
Compute: Array A, indexed by I and J, containing all the elements of B.
Model file: Unflattening 2-D to 1-D.ana (contains setup and one possible solution)
Flattening a symmetrical 2-D matrix into a 1-D vector
Given: Array A[I, J], indexed by I and J.
Compute:1-D Array B[K], containing the elements of the upper-half triangle of the matrix, but without their duplicate lower-half elements.
Model file: Flattening triangular matrix.ana
The model file contains three possible solutions (The 3rd is the preferred).
Transforming between a Monthly index and Year x Month_of_year
Similar to several of the preceeding challenges, but involving date indexes. Here you will transform from a 1-D Monthly index (spanning several years) to a 2-D Month_of_year x year array, as well as in the inverse direction. You may leverage the fact that you are dealing with dates, if that helps. Load the model file and fill in the definitions of the two undefined nodes. Many solutions exist, some of which are included in a submodule.
Model file: Month-Year-Transformations.ana
Reorganizing data
Challenge problems that re-organize data from one arrangement into another.
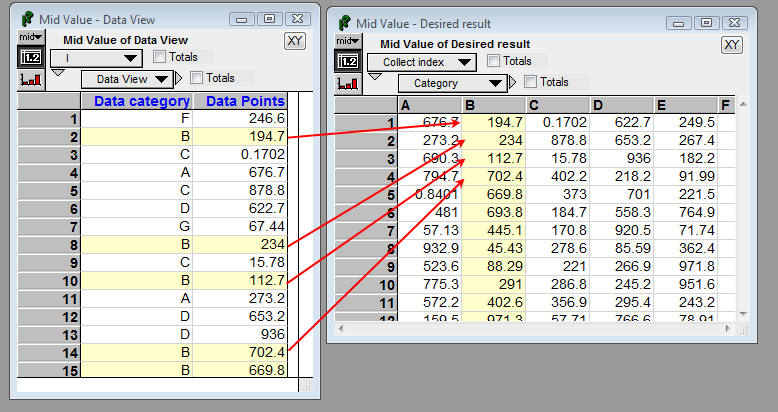
Re-organizing into categories
In this challenge, you are to organize a vector of data values into categories, as illustrated in the image shown here.
This is an advanced challenge. There are many diverse approaches possible to this problem, many of them have simple and elegant solutions, but I (a very advanced Analytica modeler) found this one to be challenging. There is a lot of room for creativity here too -- I've included four possible solutions, but I bet there are many other elegant solutions possible as well.
Because such an array of diverse approaches are possible, this challenge also presents an opportunity to explore why certain approaches are grossly inferior to others. If you find yourself writing a lot of imperative/procedural code in your models (i.e., often using assignment operators and explicit FOR loops), this may help you to learn how to dramatically improve your coding and modeling style.
This model file provides the starting data, indexes, the desired result, and a variable for you to Define. It also contains several solutions that you can study after you've found your own solution:
Model File: Rearrange data points into categories.ana
Recurrent Series
Number of Sign changes
Given a vector of numbers of varying signs (negative, zero and positive), write an expression that computes the number of consecutive sign changes preceding each cell.
The model file provides data, a node you can fill in, and one possible solution.
Flow extension
In this challenge, you are given an initial table of flows. A flow starts in on a given date as indicated by a 1 in the table, then continues or several consecutive dates, numbering the second flow date with a 2, third day with 3, etc. After the flow ends, the table contains a 0. Your challenge is to compute a new table that extends these flows so that for each flow year
- each sequence of consecutive numbers needs go to at least 5.
- If doing this means the sequence meets another sequence, the next sequence needs to go just as far, but should be renumbered appropriately.
The following image illustrates this, where the original flows are shown and the desired computed flows are indicated in red.
Note that each Flowyear column is computed independently from the others.
Start with this Flow extension challenge.ana model file.
Aggregation
Aggregate daily value to the monthly level. Combine information given at daily and monthly levels. Disaggregate (spread) monthly values to the daily level.
The attached model contains 5 challenges related in aggregation. Each module contains the challenge -- a variable you need to fill in the Definition for -- along with the variables you will use for the challenge. A "correct" solution node is given in each case, which you can look at to see what you need to compute. A solution is also given in each challenge -- don't peek at those until you've solved it yourself.
Download model: Aggregation challenges.ana
Multi-Step Hybrid Challenges
Counting Pairs
Contruct a table of all pairs of contributing factors that occur together, showing how many times the pair occurs and sorted by decreasing frequency.
Given: An array of booleans, B indexed by Failure and Factor, with a 1 indicating that the factor was a contributor to the given failure.
Compute: A table showing each pair of factors that occur together, with how many times that pair was observed to co-occur, and sorted by decreasing count.
Model file: Pair Counting.ana
The model contains the starting data, the desired result, and one possible solution broken down step-by-step. For the full challenge, find a way to compute the solution yourself without looking. If you aren't up for that, then take on the four individual steps in the solution as four smaller challenge exercises.
Tiered Billing
Some rate schedules such as tax rate schedules and utility billing schedules use a tiered rate scheme. For example, in California, Pacific Gas & Electric uses a 5-tiered billing system for residential customers for electricity usage. For a household assigned a baseline allotment of 200kWh per month, the rate pricing schedule (at the time of this writing) is as follows:
Tier 1 Tier 2 Tier 3 Tier 4 Tier 5 consumed (kWh) 0-200 201-260 261-400 401-600 over 600 rate ($/kWh) $0.12 $0.14 $0.29 $0.39 $0.44
If you were to consume 300 kWh of electricity in a given month, your bill would be determined as follows. The "first" 200kWh would be billed at $0.12/kWh, the next 60kWh at $0.14/kWh, and then the residual 40kWh at $0.29/kWh. The bill would thus be:
0.12*200 + 0.14*60 + 0.29*40 = $38
Given: A rate schedule with usage limits for each tier; an actual usage amount.
Compute: Usage amount that falls into each tier, and total price to be billed.
Model file: Tiered Billing.ana
The model file contains a rate schedule and an example usage amount. Two sample solutions are provided.
Connected components
Start with a collection of items and information about which pairs of items are touching. Your challenge is to figure out how many connected components there are, and to number each item with the ID of its connected component. Every item belongs to exactly one connected component, any two items that touch must belong to the same component, and two items are in the same component if and only if there is a path between them along touching items.
Given: An adjacency matrix.
Compute: Which connected component each item belongs to, which components numbered from 1 to n, n being the number of different connected components.
Model file: Connected components challenge.ana
The model file includes example adjacency matrices (7 different test cases), the desired solution for each, and an implementation of one possible solution. For an added challenge, implement a solution that array abstracts -- i.e., that works when Case is set to All.
This challenge is more of an algorithmic challenge, which happens to involve matrices/arrays. I am not aware of a trivial solution.

Enable comment auto-refresher