Expressing Uncertainty

Analytica makes it easy to model and analyze uncertainties even if you have minimal background

in probability and statistics. The graphs below review several key concepts from probability and statistics to help you understand the probabilistic modeling facilities in Analytica. This chapter assumes that you have encountered most of these concepts before, but possibly in the distant past. If you need more information, see “Glossary” on page 447 or refer to an introductory text on probability and statistics.

Uncertain quantity X

Choosing an appropriate distribution

With Analytica, you can express uncertainty about any variable by using a probability distribution. You can base the distribution on available relevant data, on the judgment of a knowledgeable individual, or on some combination of data and judgment. Answer the following questions about the uncertain quantity to select the most appropriate kind of distribution:

• Is it discrete or continuous?
• If continuous, is it bounded?
• Does it have one mode or more than one?
• Is it symmetric or skewed?
• Should you use a standard or a custom distribution?

Is the quantity discrete or continuous?

When trying to express uncertainty about a quantity, the first technical question is whether the quantity is discrete or continuous.

A discrete quantity has a finite number of possible values — for example, the gender of a person or the country of a person’s birth. Logical or Boolean variables are a type of discrete variable with only two values, true or false, sometimes coded as yes or no, present or absent, or 1 or 0 — for example, whether a person was born before January 1, 1950, or whether a person has ever resided in California.

A continuous quantity can be represented by a real number, and has infinitely many possible values between any two values in its domain. Examples are the quantity of an air pollutant released during a given period of time, the distance in miles of a residence from a source of air pollution, and the volume of air breathed by a specified individual during one year.

For a large discrete quantity, such as the number of humans residing within 50 miles of Disneyland on December 25, 1980, it is often convenient to treat it as continuous. Even though you know that the number of live people must be an integer, you might want to represent uncertainty about the number with a continuous probability distribution.

Conversely, it is often convenient to treat continuous quantities as discrete by partitioning the set of possible values into a small finite set of partitions. For example, instead of modeling human age by a continuous quantity between 0 and 120, it is often convenient to partition people into infants (age < 2 years), children (3 to 12), teenagers (13 to 19), young adults (20 to 40), middleaged (41 to 65), and seniors (over 65 years). This process is termed discretizing. It is often convenient to discretize continuous quantities before assessing probability distributions.

Does the quantity have bounds?

If the quantity is continuous, it is useful to know if it is bounded before choosing a distribution — that is, does it have a minimum and maximum value?

Some continuous quantities have exact lower bounds. For example, a river flow cannot be less than zero (assuming the river cannot reverse direction). Some quantities also have exact upper bounds. For example, the percentage of a population that is exposed to an air pollutant cannot be greater than 100%.

Most real world quantities have de facto bounds — that is, you can comfortably assert that there is zero probability that the quantity would be smaller than some lower bound, or larger than some upper bound, even though there is no precise way to determine the bound. For example, you can be sure that no human could weigh more than 5000 pounds; you might be less sure whether 500 pounds is an absolute upper bound.

Many standard continuous probability distributions, such as the normal distribution, are unbounded. In other words, there is some probability that a normally distributed quantity is below any finite value, no matter how small, and above any finite value, no matter how large.

Nevertheless, the probability density drops off quite rapidly for extreme values, with near exponential decay, in fact, for the normal distribution. Accordingly, people often use such unbounded distributions to represent real world quantities that actually have finite bounds. For example, the normal distribution generally provides a good fit for the distribution of heights in a human population, even though you might be certain that no person’s height is less than zero or greater than 12 feet.

How many modes does it have?

The mode of a distribution is its most probable value. The mode of an uncertain quantity is the value at the highest peak of the density function, or, equivalently, at the steepest slope on the cumulative probability distribution.

Important questions to ask about a distribution are how many modes it has, and approximately where it, or they, are? Most distributions have a single mode, but some have several and are known as multimodal distributions.

If a quantity has two or more modes, you can usually view it as a combination of two or more populations. For example, the distribution of ages in a daycare center at leaving time might include one mode at age 3 for the children and another mode at age 27 for the parents and caretakers. There is obviously a population of children and a population of parents. It is generally easier to decompose a multimodal quantity into its separate components and assess them separately than to assess a multimodal distribution. You can then assess a unimodal (single mode) probability distribution for each component, and combine them to get the aggregate distribution. This approach is often more convenient, because it lets you assess single-mode distributions, which are easier to understand and evaluate than multimodal distributions.

Is the quantity symmetric or skewed?

A symmetrical distribution is symmetrical about its mean. A skewed distribution is asymmetric. A positively skewed distribution has a thicker upper tail than lower tail; and vice versa, for a negatively skewed distribution.

Probability distributions in environmental risk analysis are often positively skewed. Quantities such as source terms, transfer factors, and dose-response factors, are typically bounded below by zero. There is more uncertainty about how large they might be than about how small they might be.

A standard or custom distribution?

The next question is whether to use a standard parametric distribution — for example, normal, lognormal, or beta — or a custom distribution, where the assessor specifies points on the cumulative probability or density function.

Considering the physical processes that generate the uncertainty in the quantity might suggest that a particular standard distribution is appropriate. More often, however, there is no obvious standard distribution to apply.

It is generally much faster to assess a standard distribution than a full custom distribution, because standard distributions have fewer parameters, typically from two to four. You should usually start by assigning a simple standard distribution to each uncertain quantity using a quick judgment based on a brief perusal of the literature or telephone conversation with a knowledgeable person. You should assess a custom distribution only for those few uncertain inputs that turn out to be critical to the results. Therefore, it is important to be able to select an appropriate standard distribution quickly for each quantity.

Defining a variable as a distribution

To define a variable as an Analytica probability distribution, first select the variable and open either the variable’s Object window or the Attribute panel (page 20) of the diagram with Definition (page 106) selected from the Attribute popup menu.

To define the distribution:

1. Click the expr menu above the definition field and select Distribution.

1. The Object Finder opens, showing the Distribution library.

1. Select the distribution you wish to use.
2. Enter the values for the parameters. You can use an expression or refer to other variables by name in the parameter fields.
3. Click OK to accept the distribution.

If the parameters of the distribution are single numbers, a button appears with the name of the distribution, indicating that the variable is defined as a distribution. To edit the parameters, click this button.

If the parameters of the distribution are complex expressions, the distribution displays as an expression. For example:

Normal((Price/Mpy) * Mpg, Mpg/10)

Entering a distribution as an expression

Alternatively, you can directly enter a distribution as an expression:

1. Set the cursor in the definition field and type in the distribution name and parameters, for example - Normal(.105, 0.015)
2. Press Alt-Enter or click the
   
   button.

You can also paste a distribution from the Distribution library in the Definition menu (see “Using a library” on page 371).

You can edit a distribution as an expression, whether it was entered as a distribution from the Distribution library or as an expression, by selecting expr from the expr menu.

Including a distribution in a definition

You can enter a distribution anywhere in a definition, including in a cell of an edit table. Thus, you can have arrays of distributions. To enter a distribution:

1. Set the insertion point where you wish to enter the distribution in the definition field or edit table cell.
2. Enter the distribution in any of the following ways:
   • Type in the name of the distribution.
   • Paste it from the Distribution library under the Definition menu.
   • Select Paste Identifier from the Definition menu to paste it from the Object Finder.
3. Type in missing parameters, or replace parameters enclosed as <<x>>.

Probabilistic calculation

Analytica performs probabilistic evaluation of probability distributions through simulation — by computing a random sample of values from the actual probability distribution for each uncertain quantity. The result of evaluating a distribution is represented internally as an array of the sample values, indexed by Run. Run is an index variable that identifies each sample iteration by an integer from 1 to Samplesize.

You can display a probabilistic value using a variety of uncertainty view options (page 29) — the mean, statistics, probability bands, probability density (or mass function), and cumulative distribution function. All these views are derived or estimated from the underlying sample array, which you can inspect using the last uncertainty view, Sample.

Example

A:= Normal(10, 2) →

Iteration (Run)

	1	2	3	4	5	6
	10.74	13.2	9.092	11.44	9.519	13.03

Tip: The values in a sample are generated at random from the distribution; if you try this example and display the result as a table, you might see values different from those shown here. To reproduce this example, reset the random number seed to 99 and use the default sampling method and random number method (see “Uncertainty Setup dialog” on page 257).

For each sample run, a random value is generated from each probability distribution in the model. Output variables of uncertain variables are calculated by calculating a value for each value of Run.

Example

B:= Normal(5, 1) →

Iteration (Run)

	1	2	3	4	5	6
	5.09	4.94	4.65	6.60	5.24	6.96

C:= A + B → Iteration (Run)

Iteration (Run)

	1	2	3	4	5	6
	15.83	18.13	13.75	18.04	14.76	19.99

Notice that each sample value of C is equal to the sum of the corresponding values of A and B. To control the probabilistic simulation, as well as views of probabilistic results, use the Uncertainty Setup dialog (page 257).

Tip: If you try to apply an array-reducing function (page 194) to a probability distribution across Run, Analytica returns the distribution’s mid value.

Example:

X:= Beta(2, 3)

Mid(X) → 0.3857 and Max(X, Run) → 0.3857

To evaluate the input parameters probabilistically and reduce across Run, use Sample() (page 301).

Example:

Max(Sample(X), Run) → 0.8892

Uncertainty Setup dialog

Use the Uncertainty Setup dialog to inspect and change the sample size, sampling method, statistics, probability bands, and samples per plot point for probability distributions. All settings are saved with your model.

To open the Uncertainty Setup dialog, select Uncertainty Options from the Result menu or Control+u. To set values for a specific variable, select the variable before opening the dialog.

The five options for viewing and changing information in the Uncertainty Setup dialog can be accessed using the Analysis option popup menu.

Uncertainty sample

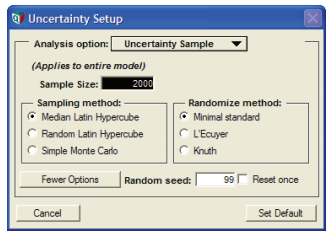
To change the sample size or sampling method for the model, select the Uncertainty Sample option from the Analysis option popup menu.

The default dialog shows only a field for sample size. To view and change the sampling method, random number method, or random seed, press the More Options button.

Sample size

This number specifies how many runs or iterations Analytica performs to estimate probability distributions. Larger sample sizes take more time and memory to compute, and produce smoother distributions and more precise statistics. See “Appendix A: Selecting the Sample Size” on page 424 for guidelines on selecting a sample size. The sample size must be between 2 and 32,000. You can access this number in expressions in your models as the system variable Samplesize.

Sampling method

The sampling method is used to determine how to generate a random sample of the specified sample size, m, for each uncertain quantity, X. Analytica provides three options:

Simple Monte Carlo

The simplest sampling method is known as Monte Carlo, named after the randomness prevalent in games of chance, such as at the famous casino in Monte Carlo. In this method, each of the m sample points for each uncertainty quantity, X, is generated at random from X with probability proportional to the probability density (or probability mass for discrete quantities) for X. Analytica uses the inverse cumulative method; it generates m uniform random values, ui, for i=1,2,...m, between 0 and 1, using the specified random number method (see below). It then uses the inverse of the cumulative probability distribution to generate the corresponding values of X,

Xi where P( ) = ui for i=1,2,...m

With the simple Monte Carlo method, each value of every random variable X in the model, including those computed from other random quantities, is a sample of m independent random values from the true probability distribution for X. You can therefore use standard statistical methods to estimate the accuracy of statistics, such as the estimated mean or fractiles of the distribution, as for example described in “Appendix A: Selecting the Sample Size” on page 424.

Median Latin hypercube (the default method)

With median Latin hypercube sampling, Analytica divides each uncertain quantity X into m equiprobable intervals, where m is the sample size. The sample points are the medians of the m intervals, that is, the fractiles

Xi where P( ) = (i-0.5)/m, for i=1,2,...m.

These points are then randomly shuffled so that they are no longer in ascending order, to avoid nonrandom correlations among different quantities.

Random Latin hypercube

The random Latin hypercube method is similar to the median Latin hypercube method, except that instead of using the median of each of the m equiprobable intervals, Analytica samples at random from each interval. With random Latin hypercube sampling, each sample is a true random sample from the distribution. However, the samples are not totally independent.

Choosing a sampling method

The advantage of Latin hypercube methods is that they provide more even distributions of samples for each distribution than simple Monte Carlo sampling. Median Latin hypercube is still more evenly distributed than random Latin hypercube. If you display the PDF of a variable that is defined as a single continuous distribution, or is dependent on a single continuous uncertain variable, using median Latin hypercube sampling, the distribution usually looks fairly smooth even with a small sample size (such as 20), whereas the result using simple Monte Carlo looks quite noisy.

If the variable depends on two or more uncertain quantities, the relative noise-reduction of Latin hypercube methods is reduced. If the result depends on many uncertain quantities, the performance of the Latin hypercube methods might not be discernibly better than simple Monte Carlo. Since the median Latin hypercube method is sometimes much better, and almost never worse than the others, Analytica uses it as the default method. Very rarely, median Latin hypercube can produce incorrect results, specifically when the model has a periodic function with a period similar to the size of the equiprobable intervals. For example:

X:= Uniform(1, Samplesize)

Y:= Sin(2*Pi*X)

This median Latin hypercube method gives very poor results. In such cases, you should use random Latin hypercube or simple Monte Carlo. If your model has no periodic function of this kind, you do not need to worry about the reliability of median Latin hypercube sampling.

Random number method

The random number method is used to determine how random numbers are generated for the probability distributions. Analytica provides three different methods for calculating a series of pseudorandom numbers.

Minimal Standard (the default method)

The Minimal Standard random number generator is an implementation of Park and Miller’s Minimal Standard (based on a multiplicative congruential method) with a Bays-Durham shuffle. It gives satisfactory results for less than 100,000,000 samples.

L’Ecuyer

The L’Ecuyer random number generator is an implementation of L’Ecuyer’s algorithm, based on a multiplicative congruential method, which gives a series of random numbers with a much longer period (sequence of numbers that repeat). Thus, it provides good random numbers even with more than 100,000,000 samples. It is slightly slower than the Minimal Standard generator.

Knuth

Knuth’s algorithm is based on a subtractive method rather than a multiplicative congruential method. It is slightly faster than the Minimal Standard generator.

Random seed

This value must be a number between 0 and 100,000,000 (10<sup>8<sup>). The series of random numbers starts from this seed value when:

• A model is opened.

• The value in this field is changed.

• The Reset once box is checked, and the Uncertainty Setup dialog is closed by clicking the Accept or Set Default button.

Rest once

Check the Reset once box to produce the exact same series of random numbers

Statistics option

To change the statistics reported when you select Statistics as the uncertainty view for a result, select the Statistics option from the Analysis option popup menu.

Probability Bands option

To change the probability bands displayed when you select Probability Bands as the uncertainty view for a result, select the Probability Bands option from the Analysis option popup menu.

Probability density option

To change how probability density is estimated and drawn, select Probability Density from the Analysis option popup menu.

Analytica estimates the probability density function, like other uncertainty views, from the underlying array of sample values for each uncertain quantity. The probability density is highly susceptible to random sampling variation and noise. Both histogramming and kernel density smoothing techniques are available for estimating the probability density from the sample, but to ultimately reduce noise and variability it may be necessary to increase sample size (for details on selecting the sample size, see “Appendix A: Selecting the Sample Size” on page 424). The following example graphs compare the two methods on the same uncertain result:

Histogram

The histogram estimation methods partition the space of possible continuous values into bins, and then tally how many samples land in each bin. The probability density is then equal to the fraction of the Monte Carlo sample landing in a given bin divided by the bin’s width. The average number of points landing in each bin determines both the smoothness of the resulting function and the resolution of the resulting plot. With more bins, a finer resolution is obtained, but since fewer points land in each bin, the amount of random fluctuation increases resulting in a noisier plot. The Samples per PDF step interval setting sizes the bin width to match the average number of points per bin.

With larger sample sizes, you can increase the Samples per PDF step interval to achieve smoother plots, since more samples will land in each bin. A number approximately equal to the square root of sample size tends to work fairly well.

You can also control how the partitioning of the space of values is performed. When Equal X axis steps is used, the range of values from the smallest to largest sample point is partitioned into equal sized bins. With this method, all bins have the same width, but the number of points falling in each bin varies. When Equal weighted probability steps is used, the bins are sized so that each bin contains approximately the same fraction of the total probability. With this method, the fraction of the sample in each bin is nearly constant, but the width of each bin varies. When Equal sample probability steps is used, the bins are partitioned so that the number of sample points in each bin is constant, with the width of each bin again varying. Equal weighted probability steps and Equal sample probability steps are exactly equivalent when standard equally-weighted Monte Carlo or Latin Hypercube sampling is being used. They differ when the Sample Weighting system variable assigns different weights to each sample along the Run index, as is sometimes employed with importance sampling, logic sampling for posterior analysis, and rare-event modeling. See “Importance weighting” on page 291.

Probability density plots using the histogram method default to the Step chart type, which emphasizes the histogram and reveals the bin placements. When desired, this can be changed to the standard line style from the Graph Setup, see “Chart Type tab” on page 86.

Smoothing

The smoothing method estimtes probability density using a technique known as Kernel Density Estimation (KDE) or Kernel Density Smoothing. This technique replaces each Monte Carlo sample with a Gaussian curve, called a Kernel, and then sums the curve to obtain the final continuous curve. Unlike a histogram, the degree of smoothness and the resolution of the plot are independent. The Smoothing factor controls the smoothness or amount of detail in the estimated PDF. The more info button next to the Smoothing radio control jumps to a page on the Analytica Wiki that elaborates in more detail on how kernel density smoothing works.

Due to the randomness of Monte Carlo sampling, estimations of probability density are often quite noisy. The Smoothing method can often provide smoother and more intuitively appealing plots than Histogram methods, but the averaging effects inherent in smoothing can also introduce some minor artifacts. In particular, Smoothing tends to increase the apparent variance in your result slightly, with a greater increase when the Smoothing factor is greater. This increase in variance is also seen as a decrease in the height of peaks. Sharp cutoffs (such as is the case with a Uniform distribution, for example) become rounded with a decaying tail past the cutoff point. And when positive-only distributions begin with a very sharp rise, the density estimate may get smoothed into a plot with a tail extending into the negative value territory.

Cumulative probability option

To change how the cumulative probability values are drawn or to change their resolution, select the respective option from the Analysis option popup menu.

Analytica estimates the cumulative distribution function, like other uncertainty views, from the underlying array of sample values for each uncertain quantity. As with any simulation-based method, each estimated distribution has some noise and variability from one evaluation to the next. Cumulative probability estimates are less susceptible to noise than, for example, probability density estimates.

The Samples per CDF plot point setting controls the average number of sample values used to estimate each point on the cumulative distribution function (CDF) curve, which ultimately controls the number of points plotted on your result.

The Equal X axis steps, Equal weighted probability steps and Equal sample probability steps control which points are used in plot of the cumulative probability. Equal X axis steps spaces points equally along the X axis. Equal weighted probability steps uses the sample to estimate a set of m+! fractiles (quantiles), Xp, at equal probability intervals, where p=0, q, 2q, ... 1, and q = 1/m. The cumulative probability is plotted at each of the points Xp, increasing in equal steps along the vertical axis. Points are plotted closer together along the horizontal axis in the regions where the density is the greatest. Equal sample probability steps plots one point each at each nth sample point, where n is the sample per CDF plot point, ignoring the weight on each sample point when they are weighted differently. The cumulative probability up to the nth point is estimated and plotted. Equal weighted probability steps and Equal sample probability steps are exactly equivalent unless unwequal sample weighting is employed (see “Importance weighting” on page 291).