Formulations that Preserve Linearity for Optimization

When creating an optimization model, there are advantages to formulating your model as a linear program (LP), avoiding non-linear relationships. Linear programs solve more robustly than non-linear programs, and usually solve faster than their non-linear counterparts even when there are mixed-integer decision variabels.

Many problems that seem non-linear at the outset can be converted into a linear formulation with sufficient ingenuity, often by changing the set of decision variables used to represent the problem and its search space, and by introducing auxilliary integer and boolean variables and auxilliary constraints. In general, this transformation is not easy and requires substantial creativity and analytical skills.

This page is devoted to cataloging various cases that come up with solutions for how these can be encoded in a linear fashion.

Piecewise linear relationships

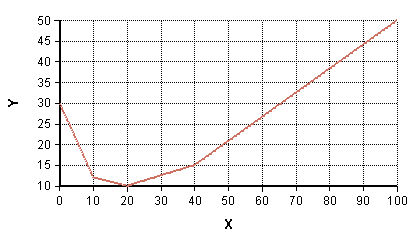
Income tax is a function of taxable income, but in the US is determined according to a piecewise-linear specification (with the slope changing at different tax brackets). In other cases, a non-linear relationship between two scalar variables can be approximated by a piecewise linear curve, as in this example:

Structured optimization in Analytica processes piecewise-linear relationships automatically for you when these appear within your model through the use of the LinearInterp function. A PWL curve is specified by a set of points, (d,r), containing the break points in the curve. In Analytica, these would be arrays d and r sharing a common index i. The result, y is then computed as LinearInterp(d,r,x,i). To be linear, the arrays d and r cannot depend on decision variables of the optimization.

Calls to LinearInterp can appear anywhere in your model. DefineOptimization processes these automatically and adds several binary and continuous auxilliary variables to the underlying optimization problem while preserving linearity.

Semi-continuous Domains

A certain power plant can either be off, or its power output is bounded 100MW and 500MW.

This type of relationship can be encoded by introducing a few auxilliary variables and constraints as follows:

Decision PowerPlantOn
Domain: Boolean()
 
Decision: PowerPlantOutput
Domain: Continuous(0,500M)
 
Constraint PowerPlantOutput_Lb := 100M
 
Constraint: Zero_When_Off
Definition: PowerPlantOutput <= PowerPlantOn * DomainUpperBound(PowerPlantOutput)
 
Constraint: Exceeds_LB_When_On
Definition: PowerPlantOn * PowerPlantOutput_Lb <= PowerPlantOutput

You then must include PowerPlantOn and PowerPlantOutput as decision variables to DefineOptimization, and Zero_When_Off and Exceeds_LB_When_On as constraints.