Difference between revisions of "Uncertainty Setup dialog"
| Line 5: | Line 5: | ||
Use the '''Uncertainty Setup''' dialog to inspect and change options to compute and display uncertain quantities. It contains five tabs/menu options: '''Uncertainty sample''' including sampling method, '''Statistics''', '''Probability bands''', '''Cumulative probability''' and '''Probability density''' views. Each is described below. The Uncertainty sample methods apply to the entire model. You can apply the rest to a single variable or as the default for the entire model. It saves all settings with your model. | Use the '''Uncertainty Setup''' dialog to inspect and change options to compute and display uncertain quantities. It contains five tabs/menu options: '''Uncertainty sample''' including sampling method, '''Statistics''', '''Probability bands''', '''Cumulative probability''' and '''Probability density''' views. Each is described below. The Uncertainty sample methods apply to the entire model. You can apply the rest to a single variable or as the default for the entire model. It saves all settings with your model. | ||
| − | To open the '''Uncertainty Setup''' dialog, select '''Uncertainty Options''' from the | + | To open the '''Uncertainty Setup''' dialog, select '''Uncertainty Options''' from the [[Result menu]] or ''Control+u''. To set values for a specific variable, select the variable before opening the dialog. |
You can select each of the five options in the '''Uncertainty Setup''' dialog from the '''Analysis option''' menu. | You can select each of the five options in the '''Uncertainty Setup''' dialog from the '''Analysis option''' menu. | ||
| Line 25: | Line 25: | ||
=== Monte Carlo sampling === | === Monte Carlo sampling === | ||
| − | The most widely used sampling method is known as Monte Carlo, named after the randomness prevalent in games of chance, such as at the famous casino in Monte Carlo. In this method, each of the m sample points for each uncertainty quantity, '''X''', is generated at random from X with probability proportional to the probability density (or probability mass for discrete quantities) for '''X'''. Analytica uses the inverse cumulative method; it generates m uniform random values, <code>u<sub>i</sub>, for i=1,2,...m</code>, between 0 and 1, using the specified random number method (see below). It then uses the inverse of the cumulative probability distribution to generate the corresponding values of '''X''', | + | The most widely used sampling method is known as Monte Carlo, named after the randomness prevalent in games of chance, such as at the famous casino in Monte Carlo. In this method, each of the m sample points for each uncertainty quantity, '''X''', is generated at random from X with probability proportional to the probability density (or probability mass for discrete quantities) for '''X'''. Analytica uses the inverse cumulative method; it generates m uniform random values, <code>u<sub>i</sub>, for i = 1, 2,...m</code>, between 0 and 1, using the specified random number method (see below). It then uses the inverse of the cumulative probability distribution to generate the corresponding values of '''X''', |
| − | :<code>X<sub>i</sub> where P( ) = u<sub>i</sub> for i=1,2,...m</code> | + | :<code>X<sub>i</sub> where P( ) = u<sub>i</sub> for i = 1, 2,...m</code> |
With the simple Monte Carlo method, each value of every random variable X in the model, including those computed from other random quantities, is a sample of m independent random values from the true probability distribution for X. You can therefore use standard statistical methods to estimate the accuracy of statistics, such as the estimated mean or fractiles of the distribution, as for example described in [[Selecting the Sample Size]]. | With the simple Monte Carlo method, each value of every random variable X in the model, including those computed from other random quantities, is a sample of m independent random values from the true probability distribution for X. You can therefore use standard statistical methods to estimate the accuracy of statistics, such as the estimated mean or fractiles of the distribution, as for example described in [[Selecting the Sample Size]]. | ||
| Line 34: | Line 34: | ||
Median Latin hypercube sampling is the default method: It divides each uncertain quantity '''X''' into m equiprobable intervals, where m is the sample size. The sample points are the medians of the m intervals, that is, the fractiles | Median Latin hypercube sampling is the default method: It divides each uncertain quantity '''X''' into m equiprobable intervals, where m is the sample size. The sample points are the medians of the m intervals, that is, the fractiles | ||
| − | :<code>X<sub>i</sub> where P( ) = (i-0.5)/m, for i=1,2,...m.</code> | + | :<code>X<sub>i</sub> where P( ) = (i - 0.5)/m, for i = 1, 2,...m.</code> |
These points are then randomly shuffled so that they are no longer in ascending order, to avoid nonrandom correlations among different quantities. | These points are then randomly shuffled so that they are no longer in ascending order, to avoid nonrandom correlations among different quantities. | ||
| Line 51: | Line 51: | ||
This median Latin hypercube method gives very poor results. In such cases, you should use random Latin hypercube or simple Monte Carlo. If your model has no periodic function of this kind, you do not need to worry about the reliability of median Latin hypercube sampling. | This median Latin hypercube method gives very poor results. In such cases, you should use random Latin hypercube or simple Monte Carlo. If your model has no periodic function of this kind, you do not need to worry about the reliability of median Latin hypercube sampling. | ||
| − | |||
=== Random seed === | === Random seed === | ||
Revision as of 15:46, 17 May 2016
_
_
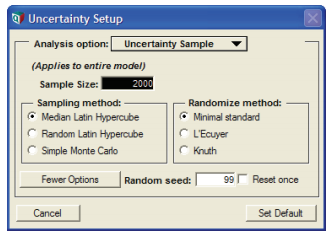
Use the Uncertainty Setup dialog to inspect and change options to compute and display uncertain quantities. It contains five tabs/menu options: Uncertainty sample including sampling method, Statistics, Probability bands, Cumulative probability and Probability density views. Each is described below. The Uncertainty sample methods apply to the entire model. You can apply the rest to a single variable or as the default for the entire model. It saves all settings with your model.
To open the Uncertainty Setup dialog, select Uncertainty Options from the Result menu or Control+u. To set values for a specific variable, select the variable before opening the dialog.
You can select each of the five options in the Uncertainty Setup dialog from the Analysis option menu.
Uncertainty sample
The default dialog shows only a field for sample size. To view and change the sampling method, random number method, or random seed, press the More Options button.
Sample size: This number specifies how many runs or iterations Analytica performs to estimate probability distributions. Larger sample sizes take more time and memory to compute, and produce smoother distributions and more precise statistics. See Selecting the Sample Size for guidelines on selecting a sample size. The sample size must be between 2 and 32,000. You can access this number in expressions in your models as the system variable SampleSize.
Sampling method
The sampling method is used to determine how to generate a random sample of the specified sample size, m, for each uncertain quantity. Analytica offers three options: Monte Carlo, Median Latin hypercube (the default), and Random Latin hypercube sampling methods:
Monte Carlo sampling
The most widely used sampling method is known as Monte Carlo, named after the randomness prevalent in games of chance, such as at the famous casino in Monte Carlo. In this method, each of the m sample points for each uncertainty quantity, X, is generated at random from X with probability proportional to the probability density (or probability mass for discrete quantities) for X. Analytica uses the inverse cumulative method; it generates m uniform random values, ui, for i = 1, 2,...m, between 0 and 1, using the specified random number method (see below). It then uses the inverse of the cumulative probability distribution to generate the corresponding values of X,
Xi where P( ) = ui for i = 1, 2,...m
With the simple Monte Carlo method, each value of every random variable X in the model, including those computed from other random quantities, is a sample of m independent random values from the true probability distribution for X. You can therefore use standard statistical methods to estimate the accuracy of statistics, such as the estimated mean or fractiles of the distribution, as for example described in Selecting the Sample Size.
Median Latin hypercube
Median Latin hypercube sampling is the default method: It divides each uncertain quantity X into m equiprobable intervals, where m is the sample size. The sample points are the medians of the m intervals, that is, the fractiles
Xi where P( ) = (i - 0.5)/m, for i = 1, 2,...m.
These points are then randomly shuffled so that they are no longer in ascending order, to avoid nonrandom correlations among different quantities.
Random Latin hypercube
The random Latin hypercube method is similar to the median Latin hypercube method except that, instead of using the median of each of the m equiprobable intervals, it samples at random from each interval. With random Latin hypercube sampling, each sample is a true random sample from the distribution, as in simple Monte Carlo. However, the samples are not totally independent because they are constrained to have one sample from each of the n intervals.
Choosing a sampling method
The advantage of Latin hypercube methods is that they provide more even distributions of samples for each distribution than simple Monte Carlo sampling. Median Latin hypercube is still more evenly distributed than random Latin hypercube. If you display the PDF of a variable that is defined as a single continuous distribution, or is dependent on a single continuous uncertain variable, using median Latin hypercube sampling, the distribution usually looks fairly smooth even with a small sample size (such as 20), whereas the result using simple Monte Carlo looks quite noisy.
If the variable depends on two or more uncertain quantities, the relative noise-reduction of Latin hypercube methods is reduced. If the result depends on many uncertain quantities, the performance of the Latin hypercube methods might not be discernibly better than simple Monte Carlo. Since the median Latin hypercube method is sometimes much better, and almost never worse than the others, Analytica uses it as the default method. Very rarely, median Latin hypercube can produce incorrect results, specifically when the model has a periodic function with a period similar to the size of the equiprobable intervals. For example:
X := Uniform(1, Samplesize)Y := Sin(2*Pi*X)
This median Latin hypercube method gives very poor results. In such cases, you should use random Latin hypercube or simple Monte Carlo. If your model has no periodic function of this kind, you do not need to worry about the reliability of median Latin hypercube sampling.
Random seed
This value must be a number between 0 and 100,000,000 (108). The series of random numbers starts from this seed value when:
- A model is opened.
- The value in this field is changed.
- You check the Reset once box, and close the Uncertainty Setup dialog by clicking Accept or Set Default.
Reset once
Check the Reset once box to produce the exact same series of random numbers
Random number method
The random number method is used to determine how random numbers are generated for the probability distributions. It is extremely rare that any Analytica user will need to worry about the differences between these methods, and use anything other than the default method. For those that do, it offers three different options:
- Minimal Standard (the default method): The Minimal Standard random number generator is an implementation of Park and Miller’s Minimal Standard (based on a multiplicative congruential method) with a Bays-Durham shuffle. It gives satisfactory results for less than 100,000,000 samples.
- L’Ecuyer: The L’Ecuyer random number generator is an implementation of L’Ecuyer’s algorithm, based on a multiplicative congruential method, which gives a series of random numbers with a much longer period (sequence of numbers that repeat). Thus, it provides good random numbers even with more than 100,000,000 samples. It is slightly slower than the Minimal Standard generator.
- Knuth: Knuth’s algorithm is based on a subtractive method rather than a multiplicative congruential method. It is slightly faster than the Minimal Standard generator.
Statistics option
To change the statistics reported when you select Statistics as the uncertainty view for a result, select the Statistics option from the Analysis option popup menu.
Probability Bands option
To change the probability bands displayed when you select Probability Bands as the uncertainty view for a result, select the Probability Bands option from the Analysis option popup menu.
Probability density option
To change how probability density is estimated and drawn, select Probability Density from the Analysis option popup menu.
Analytica estimates the probability density function, like other uncertainty views, from the underlying array of sample values for each uncertain quantity. The probability density is highly susceptible to random sampling variation and noise. Both histogramming and kernel density smoothing techniques are available for estimating the probability density from the sample, but to ultimately reduce noise and variability it may be necessary to increase sample size (for details on selecting the sample size, see Selecting the Sample Size). The following example graphs compare the two methods on the same uncertain result:
Histogram: The histogram estimation methods partition the space of possible continuous values into bins, and then tally how many samples land in each bin. The probability density is then equal to the fraction of the Monte Carlo sample landing in a given bin divided by the bin’s width. The average number of points landing in each bin determines both the smoothness of the resulting function and the resolution of the resulting plot. With more bins, a finer resolution is obtained, but since fewer points land in each bin, the amount of random fluctuation increases resulting in a noisier plot. The Samples per PDF step interval setting sizes the bin width to match the average number of points per bin. With larger sample sizes, you can increase the Samples per PDF step interval to achieve smoother plots, since more samples will land in each bin. A number approximately equal to the square root of sample size tends to work fairly well.
You can also control how the partitioning of the space of values is performed. When Equal X axis steps is used, the range of values from the smallest to largest sample point is partitioned into equal sized bins. With this method, all bins have the same width, but the number of points falling in each bin varies. When Equal weighted probability steps is used, the bins are sized so that each bin contains approximately the same fraction of the total probability. With this method, the fraction of the sample in each bin is nearly constant, but the width of each bin varies. When Equal sample probability steps is used, the bins are partitioned so that the number of sample points in each bin is constant, with the width of each bin again varying. Equal weighted probability steps and Equal sample probability steps are exactly equivalent when standard equally-weighted Monte Carlo or Latin Hypercube sampling is being used. They differ when the Sample Weighting system variable assigns different weights to each sample along the Run index, as is sometimes employed with importance sampling, logic sampling for posterior analysis, and rare-event modeling. See Importance weighting.
Probability density plots using the histogram method default to the Step chart type, which emphasizes the histogram and reveals the bin placements. When desired, this can be changed to the standard line style from the Graph Setup, see Chart Type tab.
Smoothing: The smoothing method estimates probability density using a technique known as Kernel Density Estimation (KDE) or Kernel Density Smoothing. This technique replaces each Monte Carlo sample with a Gaussian curve, called a Kernel, and then sums the curve to obtain the final continuous curve. Unlike a histogram, the degree of smoothness and the resolution of the plot are independent. The Smoothing factor controls the smoothness or amount of detail in the estimated PDF. The more info button next to the Smoothing radio control jumps to a page on the Analytica Wiki that elaborates in more detail on how kernel density smoothing works.
Due to the randomness of Monte Carlo sampling, estimations of probability density are often quite noisy. The Smoothing method can often provide smoother and more intuitively appealing plots than Histogram methods, but the averaging effects inherent in smoothing can also introduce some minor artifacts. In particular, Smoothing tends to increase the apparent variance in your result slightly, with a greater increase when the Smoothing factor is greater. This increase in variance is also seen as a decrease in the height of peaks. Sharp cutoffs (such as is the case with a Uniform distribution, for example) become rounded with a decaying tail past the cutoff point. And when positive-only distributions begin with a very sharp rise, the density estimate may get smoothed into a plot with a tail extending into the negative value territory.
Cumulative probability option
To change how the cumulative probability values are drawn or to change their resolution, select the respective option from the Analysis option == popup menu.
Analytica estimates the cumulative distribution function, like other uncertainty views, from the underlying array of sample values for each uncertain quantity. As with any simulation-based method, each estimated distribution has some noise and variability from one evaluation to the next. Cumulative probability estimates are less susceptible to noise than, for example, probability density estimates.
The Samples per CDF plot point setting controls the average number of sample values used to estimate each point on the cumulative distribution function (CDF) curve, which ultimately controls the number of points plotted on your result.
The Equal X axis steps, Equal weighted probability steps and Equal sample probability steps control which points are used in plot of the cumulative probability. Equal X axis steps spaces points equally along the X axis. Equal weighted probability steps uses the sample to estimate a set of m+! fractiles (quantiles), Xp, at equal probability intervals, where p=0, q, 2q, ... 1, and q = 1/m. The cumulative probability is plotted at each of the points Xp, increasing in equal steps along the vertical axis. Points are plotted closer together along the horizontal axis in the regions where the density is the greatest. Equal sample probability steps plots one point each at each nth sample point, where n is the sample per CDF plot point, ignoring the weight on each sample point when they are weighted differently. The cumulative probability up to the nth point is estimated and plotted. Equal weighted probability steps and Equal sample probability steps are exactly equivalent unless unequal sample weighting is employed (see Importance weights).
See Also
- Uncertainty Setup Dialog
- Expressing Uncertainty
- Tutorial: Displaying alternative uncertain views
- CDF
- Gaussian
- Probability distributions
- Distribution Densities Library
- Kernel Density Smoothing
- Importance weights







Enable comment auto-refresher