VectorCrossProduct

new to Analytica 5.0

VectorCrossProduct( u, v, I )

Computes the vector cross product of two vectors in 3-dimensional space (or in 7-dimensional space). The vectors «u» and «v» are both indexed by index «I», and «I» must have an index length of 3 or 7. The result is also indexed by «I» and has the following properties (up to numeric round-off):

• For a fixed «v», the resulting vector varies linearly with «u».
• For a fixed «u», the resulting vector varies linearly with «v».
• The resulting vector is perpendicular to both «u» and «v».

  Hence, up to numeric round-off, the dot products, Sum(u*w,I) and Sum(v*w,I) are zero.

• The length of the vector is equal to the area of the parallelogram spanned by «u» and «v».

Examples

[x, y] →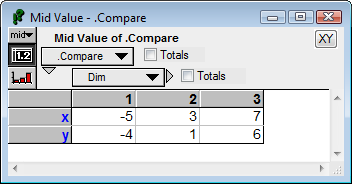

VectorCrossProduct(x,y,Dim) →

x1 := Array(J, [1,0,0] )

x2 := Array(J, [0,1,0] )

VectorCrossProduct(x1, x2, J) → Array( J, [0, 0, 1] )

x3 := Array(J, [3,0,0] )

x4 := Array(J, [0,5,0] )

VectorCrossProduct(x3, x4, J) → Array( J, [0, 0, 15] )

Why only 3- or 7-dimensional space?

Students of linear algebra learn about the vector cross product in Euclidean 3-space, and many wonder whether the operator generalizes to higher-dimensional spaces. When we assume that the essence of a cross product are the bullet points listed above (bi-linearity, orthogonality, and area equal to the parallelogram), then it turns out that a function with those properties only exists in 3- and 7- dimensional Euclidean spaces. A proof of this is given in Massey (1983).

In practice, when using this, you will probably be working with 3-dimensional space.

See also

• W. S. Massey (Dec. 1983), "[http://www-bcf.usc.edu/~lototsky/MATH226/Handts/CrossProduct-3or7dim.pdf Cross products of vectors in higher dimensional Euclidean spaces," The American Mathematical Monthly, 90(10):697-701
• Sum
• DotProduct -- Note: Usually in Analytica, Sum(u*v,I) is used for the dot-product. But there is also another function with the name DotProduct.