Parametric analysis
| Release: |
• 4.6 • 5.0 • 5.1 • 5.2 • 5.3 • 5.4 • • 6.0 • 6.1 • 6.2 • 6.3 • 6.4 • 6.5 • 6.6 |
|---|
A potent source of insight into a model is to examine how it behaves as you vary one or more of its input parameters. Analytica makes it simple to analyze model behavior in this way. All you have to do is to set a list of alternative values to each input parameter. When you view the result of any output, it displays a table or graph of how it varies for each combinations of the input parameters.
Set the input parameters
The first step is to select one or more input variables as parameters and to assign each parameter a list of possible values.
Which input parameters to vary?
Usually, you'll want to explore the effects of changing any Decision variables to see how they affect the results, and especially how you can improve the Objective variable(s) (if you have one). You should also consider uncertain variables, whether you have defined them as Chance variables or not. You should focus on the variables whose range of variation you expect to have the largest effect on the results. You can use range sensitivity analysis (Tornado chart) or importance analysis to find out which those variables are empirically, since our intuitions about what's important are often wrong. In fact, a key reason to be doing sensitivity analysis is to improve our intuitions!
How many input parameters to vary?
It's usually best to start very simply by treating just one or two variables parametrically. After exploring their results, you might add another parameter, or replace a parameter with little effect by one that may have a larger effect. It's rarely helpful to vary more than three or four parameters together. The computational effort goes up exponentially with the number of parametric variables, which is an obstacle for large models. More important, it becomes challenging to understand the results when varying more than 3 or 4 parameters in combination -- and understanding is the main goal of the exercise!
How many values to assign to each parameter?
Typically, you might set three values for each parameter — a low, medium, and high value. That let's you see if it has a nonlinear effect on results. If you find a strong nonlinear effect with three values, you might add some more values to explore the effects in more detail. If a variable is discrete with a defined menu of options using a Choice() function, you can select All to compare the effects of all options (if the Choice menu was set up to allow All). If a Choice() has a large number of options, you might redefine it to use MultiChoice(), so that you can select a few options for comparison, but not All.
Create a list of values
If the input parameter is defined as a single number or probability distribution, you can change it to a list:
- Ensure you are in edit mode (
 )
) - Select the variable by clicking its node in the influence diagram.
- Display the variable’s definition by clicking the Expression Hover icon (
 ), or typing Control+e, or clicking the Expression button
), or typing Control+e, or clicking the Expression button  in the tools palette.
in the tools palette. - Click the expr (Expression) menu above the definition and select the List option. (Do not select the List of Labels option.)


- Click OK when a dialog asks for confirmation.
- When it shows a list with one cell containing the old definition, click that cell to select it.

- Type in the lowest value for the variable.
- Press Enter and type in the next value.
- Repeat step 7 until you have all the values you want.

For more see Editing a list.
To create a list of successive integers, use the .. operator, for example:
Decision Year := 2000 .. 2010
To create a list of of numbers with spacing other than 1, use the Sequence() function, for example:
Decision Decades := Sequence(2000, 2050, 10)
Typically you can start a parametric analysis by varying just one input variable, the one you expect to be most important. Add other variables one at a time, in order of their expected importance. If a variable turns out to have little effect, you can restore it to its original value or probability distribution. If you have many inputs whose effects on model behavior you would like to explore, vary just a few at a time, rather than trying to vary them all simultaneously.
Interpret the results of Parametric analysis
After setting one or more input parameters to a list of values, the value of any downstream variable that depends on them automatically becomes an array indexed by those parameters, with a value for each combination. If your model has an objective, you might start by looking at that variable.
- Select the variable you wish to view by clicking its node in the diagram.
- View its result in the usual ways, including clicking the "Result" popup icon next to the node, pressing Control+r", or clicking Result button
 in the Toolbar. The result displays as a table or graph.
in the Toolbar. The result displays as a table or graph.
The result is an array with a dimension for each input parameter that you have varied (in this example, Buying price and Appreciation rate). If an input parameter does not appear as a dimension of the result, its tells you that the result variable is not affected by that parameter. The result may also have other dimensions that are not input parameters you have varied — for example, Time for a dynamic model.
It is usually best to look first at the result graph to see the model’s general behavior. You need to look only at the result table if you want to see the precise numerical values. If you are varying more than one input parameter, try rearranging the dimensions (see Index selection to get additional insights into model behavior).
Understand model behavior
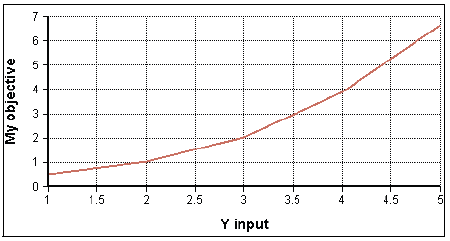
By examining result graphs, you can learn if each input affects the output, if the effect is linear or non-linear, and if there are interactions among inputs in their effect on the output. Below are some typical graph patterns and their qualitative interpretations.
- A horizontal line shows that changes in the input over the specified range have no effect on the output.

- A straight line shows that the output depends linearly on the input (assuming the input has more than two different values.)

- A bent or curved line shows a nonlinear dependence. Does the sensitivity (slope) increase or decrease with increasing value of the variable?
Understand unexpected behavior
You may find the model behaves in an unexpected way. A variable you expected to be important has little or no effect on the results. One you didn't expect to be important, has a large effect. Or a variable has an effect that is in the opposite direction to what you expected. It's import to dig into to find out why. It might be simply a bug in the model. Or it might be a "bug" in your intuition about what to expect. Either way, you need to find the source of the problem.
In Analytica, you can easily look at intermediate variables between the input(s) and the output(s) to see how these unexpected behaviors arise. You can work forward from an input towards the output, or backward from the output towards the inputs. Usually, the reason for unexpected behavior will quickly become clear to you. If you find a bug, in that the model isn't implementing the intended relationship, you can then fix it. Or if the problem is in your mental model from which you derive your intuitions, you may get a new and valuable insight, and so develop a deeper understanding of the system it represents. And that's one of the big reasons for building models in the first place. Once you've truly understood the issue, you may explain the new insight and understanding to your collaborators or clients.
See Also
- Tutorial: Performing parametric (sensitivity) analysis
- Using Parametric Analysis with Optimization
- Using Parametric Analysis: Airline NLP Module 2
- Selective Parametric Analysis
- Choosing a method for sensitivity analysis


Enable comment auto-refresher