Dawson
Dawson(x)
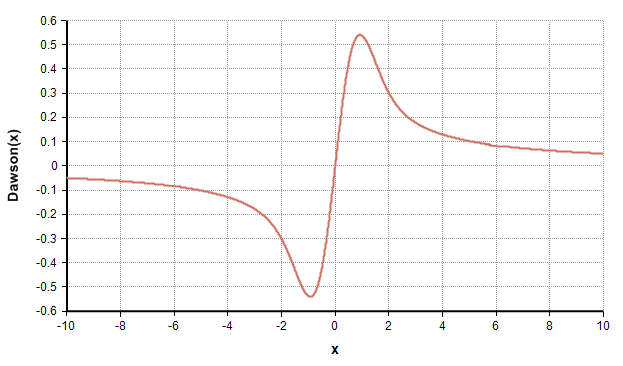
The Dawson function, or Dawson Integral, is a function defined on both real numbers and complex numbers, involving the integral of [math]\displaystyle{ e^{t^2} }[/math], but scaled by [math]\displaystyle{ e^{-x^2} }[/math] so that you don't encounter numeric overflow. It is closely related to the Erf, Faddeeva and CumNormal functions. In mathematical texts, it is often written as [math]\displaystyle{ F(x) }[/math] or [math]\displaystyle{ D_+(x) }[/math].
The Dawson function is defined as
- [math]\displaystyle{ Dawson(x) = e^{-x^2} \int_0^x e^{t^2} dt }[/math]
The [math]\displaystyle{ e^{t^2} }[/math] term appears in many mathematical and statistical contexts, but creates numeric difficulties since [math]\displaystyle{ e^{t^2} }[/math] overflows the largest double floating point when t ≥ 27. When you encounter this situation, you can often get your computation to succeed, without pushing the numeric limits, by reformulating the calculation in terms of the Dawson function.
Erfi(x)
The Dawson function can be interpreted as a scaled version of the [math]\displaystyle{ erfi(x) }[/math] function, which the relationship between the two given as
- [math]\displaystyle{ erfi(x) = {2\over\sqrt\pi} e^{x^2} D(x) }[/math]
The [math]\displaystyle{ erfi(x) }[/math] function, which is used occasionally in mathematical publication, is not a built-in function in Analytica; however, if you have an application that uses erfi, you should almost always implement your algorithm using Dawson instead, otherwise you are likely to experience numeric overflow.


Enable comment auto-refresher